[확률통계] 3. 확률변수의 정의

http://www.kocw.net/home/cview.do?cid=a2881d53f7ea3252 

확률 및 통계

 

---

• random experiment로 부터 얻은 각 결과를 real value로 mapping할 때
  • real value를 함수 표기로 표현 -> random variable
  • ex) tossing a coin
    • 앞면이 나올 확률 H, 뒷면이 나올 확률 T
    • 이것은 숫자가 아님.
    • 근데 이것을 H=1, T=0 즉, 실수값으로 매핑.
    • 이때 1과 0을 random variable이라고 한다.
  • 확률 개념을 함수로 다뤄보자!
    • P(A) -> P(x), x가 random variable
  • ex) tossing two coins
    • 앞면이 나오는 횟수를 random variable로 정한다면
    • 0 => {TT}, P(0) = P({TT})=1/4
    • 1 => {HT, TH}, P(1) = 1/2
• 좀 더 일반화 시켜보면,
  
  • RV : X, Y, Z 대문자로 사용.
  • RV X에서의 특정 값은 : x, y, z 소문자로 사용.

 

2.3 Event Defined by RV

• $A_x$를 event라 하면,
  • $A_x=\{w| X(w)=x\}$
  • 결과를 원소로 갖는데, RV 매핑을 했을 때 특정 value x로 매핑되는 집합.
  • ex) 위 tossing event에서 $A_0=\{TT\}, \ A_1=\{HT, TH\}$
• $P(A_x)=P_x(X=x)
  • RV가 x가 될 확률과 같음.
  • 즉, $P(A_1)이나 P(1)이나 같다.
• $P(a\lt X \le b)=P(A)$라 하면
  • $A =\{w|a \lt X(w) \le b\}$
  • 즉, w라는 output을 가지는 데, 그 output을 RV X에 매핑했을 때, 오른쪽 조건을 만족하는 집합
  • ex) $P(X\le 1) = P(\{TT, HT, TH\}) = \frac{3}{4}$

 

2.4 Distribution Functions

• Cumulative Distributin Function(CDF)
  • 누적 분포 함수
  • $F_X(x)$, Random Variable(RV) X를 가지고, 특정 값 x로 매핑 되는 누적 분포 함수.
  • $F_X(x)=P(X \le x)$, RV X들이 특정 x보다 작거나 같을 확률.
  • 확률을 누적해서 만들어지는 함수 -> 누적확률. 

CDF의 특성

• if $x_1 \lt x_2$ ->$F_X(x_1) \le F_X(x_2)$
  •  equal if $P(x_1<X<x_2) = 0$
• $ 0 \le F_X(x) \le 1$
• $F_X(\infty) = lim x->\infty F_X(x) = 1$
• $F_X(-\infty) = lim x -> \infty F_X(x) = 0$
• $P(a \lt X \le b) = F_X(b) - F_X(a)$
• $P(X \gt a) = 1 - F_X(a)$
• Continuous한 경우와 discrete한 RV랑 equality부분에서 잘 구분해주어야한다.
  • CDF의 특성을 활용하려면 $ \le b$부분을 확인하고 적용해야한다.

예제

**$P(X=\frac{1}{4})=0$, continuous한 곳에서는 이러한 $le$와 $lt$가 차이가 없고, discrete한 부분, 0에서와 같이 갑자기 튀어오르는 부분에서는 equality가 확률에 차이를 준다.

 

2.5 Discrete RV

• 연속적이지 않음.

Probability Mass Function(PMF)

• Discrete Random variable 하나 하나에 대한 함수
• $P_X(x) = Prob(X=x)$
• $F_X(x) = P(X \le x) = \Sum_{x_i \le x} P_X(x_i)$ -> discrete에서의 cdf

예제

$\delta (x)$

Discrete 환경에서 개별적인 값들을 함수처럼 쓰고 싶다!

높이가 1이고, x가 0일 때 discrete하게 $\delta (x)$라고 정의.

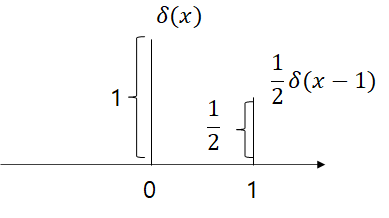
$f(x) = \frac{3}{2}\delta (x+2) + \delta(x) + \frac{1}{2} \delta(x-1)$

$\delta(x) = 1 \ \ \ if \ x=0 \ else \ 0$

 

예제

---

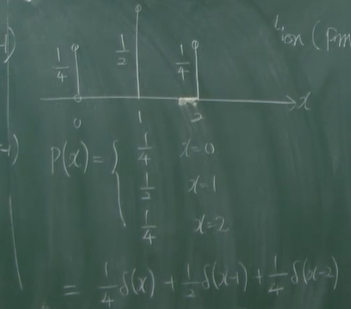
discrete RV, 특정 값들의 확률 값들이 존재한다.

하지만 다음 시간에 배울 continuous RV에서는 특정 값들의 확률이 존재하지 않는다고 한다.

대신에 확률 밀도를 사용하여 확률을 정의.