2022. 11. 29. 03:25ㆍ논문리뷰/Adversarial Attack
최근 논문 작업과 수업 등의 일들이 겹치면서 오랫만에 논문 리뷰 글을 쓰게 되었다.
이번에 리뷰할 논문은 "Patch-Fool: Are Vision Transformers Always Robust Against Adversarial Perturbations?" 이라는 제목의 논문이고, 본인이 Adversarial Attack과 Vision Transformer (ViT)에 관심이 있는 만큼 ViT의 adversarial robustness에 대한 내용을 담고 있다.
https://arxiv.org/abs/2203.08392
Patch-Fool: Are Vision Transformers Always Robust Against Adversarial Perturbations?
Vision transformers (ViTs) have recently set off a new wave in neural architecture design thanks to their record-breaking performance in various vision tasks. In parallel, to fulfill the goal of deploying ViTs into real-world vision applications, their rob
arxiv.org
1. Introduction
Vision Transformer (ViT) 관련 논문의 첫 글에 매번 나오는 내용이지만 최근 ViT가 여러 분야에서 Convolutional Neural Network (CNN)을 뛰어넘는 성능을 보여주고 있다. CNN도 마찬가지이지만 ViT를 실생활에 적용시키기 위해서는 보안적인 측면을 고려해볼 필요가 있다. 특히 보안이 중요시되는 금융이나 개인정보와 같은 application에 딥러닝을 적용하려고 할 때 "딥러닝이 과연 보안적으로 안정한지", 즉 신뢰도를 보장해야만 한다.
처음부터 딥러닝이 security 측면에서 매우 강했다면 문제가 없겠지만 안타깝게도 아주 간단한 방법으로도 딥러닝의 성능을 대폭적으로 낮출 수 있다는 것이 여러 논문을 통해 증명되었다. Attack에 대해 좀 더 알고 싶다면 다음 글을 참조하면 좋다.
https://aistudy9314.tistory.com/37
[논문리뷰] FGSM:Explaining and harnessing adversarial examples
최근 Adversarial attack에 대한 논문을 읽고 정리하는 중이다. 이전에 접해본 적이 없는 분야이기 때문에 헷갈리는 부분도 많고, 잘못 이해한 부분이 있을 수 있으니 댓글로 알려주길 바란다. 첫번째
aistudy9314.tistory.com
CNN과 ViT 모두 adversarial attack을 통해 공격할 수 있다면 다음과 같은 질문을 떠오를 것이다.
CNN과 ViT 중 어떤 model architecture가 더 attack에 강할까? 즉 security 측면에서 advantage가 있을까?
위와 같은 질문에 답하기 위해서 여러 논문들이 다양한 측면에서 두 아키텍처의 adversarial robustness를 비교하는 실험들을 하였는데, 전반적으로 ViT가 CNN보다 adversarial attacks에 대해 robust하다라는 결과를 보여준다. 하지만 이 실험들에서 사용한 attack들은 모두 CNN을 겨냥하여 그에 맞게 design된 methods임을 감안하면, 과연 ViT에도 같은 attack을 적용하는게 fair할까? 라는 의문이 든다.
그렇다면 perturbation을 어떻게 design해야 ViT를 CNN보다 더 vulnerable하게 만들 수 있을까?
이 질문이 이 논문의 핵심이자 목표라고 말할 수 있겠다.
2. PATCH-FOOL
이름에서 알 수 있듯이, 이전의 attack methods들이 pixel level에서 공격하도록 design되었다면 PATCH-FOOL은 ViT를 효과적으로 fool하기 위해서 patch level로 공격하도록 design한 attack이라할 수 있겠다.
CNN은 픽셀 단위로 kernel을 거쳐가면서 conovlution 연산이 이루어지지만 vision transformer는 patch embedding을 통해 pixel을 patch 단위로 분할 하고 이들 간의 patch-wise attention을 하기 때문에, 이 patch에 집중하여 공격을 한다는 동기가 매우 일리있다는 생각이 든다.

논문에서 기존 attack (PGD)과 Patch-Fool attack에 대한 attention map을 visualization 했을 때의 예제인데, PGD의 경우 original image와 비교해서 큰 차이가 없지만 Patch-Fool은 확연하게 차이나는 것을 볼 수 있다 (특정 patch에 크게 attention 되는 것으로 보인다).
2.1 Objective Formulation
$$argmax_{1 \le p \le n, \ E \in \mathbb{R}^{n \times d}} J(X+\mathbb{I}_p \odot E, y)$$
$X$는 $n \times d$ 차원의 input image patches, $y$는 grount truth label, $E$는 adversarial perturbation, $\mathbb{I}$는 $i \ne p$면 0, $i = p$면 1인 one-hot vector, $a \odot B = [a \circ b_1, \dots, a \circ b_d]$, $\circ$는 Hardmard product를 나타낸다.
여러가지 notation이 겹쳐서 수식으로 설명하기 어려운데 간단하게 설명해보면, 원래 이미지 $X$에다 patch selection 과정을 통해서 결정된 patches들에 대한 perturbation ($\mathbb{I}_p \odot E$)를 더한 이미지의 prediction 값과 ground truth $y$의 차이가 커지도록 하는 것이다.
더 간단히 말하면 그냥 특정 방법으로 영향력이 높은 patch를 선택해서 해당 patches에만 perturbation을 가하고 이 이미지의 prediction이 ground truth 값과 달라지도록 만들자! 이다 ㅎㅎ..
Attention-aware Patch Selection
위에서 말했 듯이 모든 patches를 공격하는 것이 아니라 (그렇게 되면 기존 attack 방법과 별다른 차이가 없으므로...) 결과 값에 영향을 많이 주는 몇 개의 patches을 선택하여 공격해야하기 때문에 patch selection이라는 과정이 필요하다.
$\alpha^{(l, h,i)} = [\alpha_1^{(l, h, i)}, \dots, \alpha_n^{(l, h, i)}] \in \mathbb{R}^n$를 $l$번째 layer의 $h$번째 head에 있는 $i$번째 token의 attention distribution이라고 해보자.
$l$번째 layer에 대해서
$$s^{(l)}_j = \sum_{h, i} \alpha^{(l, h, i)}_j$$
라 하면 $s^{(l)}_j$는 다른 tokens들에 대해서 $l$번째 layer의 $j$번째 token의 importance를 measure할 수 있는 값이 된다.
식은 약간 어려워 보일 수 있지만 그냥 $l$번째 layer에서 $j$번째 token과 모든 다른 token들과의 correlation (attention 결과)들을 모든 head에 대해 sum한 값이라고 보면 된다. 그리고 $argmax_j s^{(l)}_j$를 취해서 가장 contribution이 큰 patch를 선택하게 된다.
**논문에서는 $l=5$를 default로 한다.
Optimize $E$ via Attention-aware Loss
이번 section은 adversarial perturbation $E$를 구하기 위한 loss function에 대한 내용을 다룬다.
논문에서는 adversarial example $\tilde{X}$외에도 attention-aware loss term을 추가하였다.
$$J^{l}_{ATTN}(\tilde{X}, p)=\sum_{h,i} \alpha_p^{(l, h, i)}$$
이는 perturb된 patch p와 다른 patches간의 attention score가 높아지는 방향으로 optimize하는 텀이다. 즉, 다른 patches가 이 attacked patch p에 영향을 크게 받도록 하는 term이라고 할 수 있겠다.
최종 loss는 다음과 같다.
$$J(\tilde{X}, y, p)=J_{CE}(\tilde{X}, y) + \alpha J^{(l)}_{ATTN}(\tilde{X}, p)$$
**$\alpha$는 두 term간의 weight를 조절하는 하이퍼 파라메터 이다.
논문에서는 두 loss term간의 gradient conflict를 피하기 위해서 PCGrad라는 방법을 사용하는데, 필자도 읽어본 적이 없는 논문이라 정확한 방법은 잘 모르겠는데, update of perturbation $E$가 다음과 같이 구해진다고 한다.
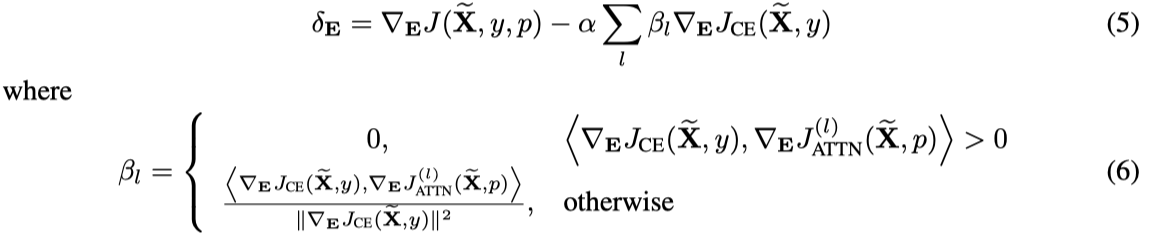
딱히 중요한 내용은 아니므로 구체적인 설명은 생략하도록 하겠다.
2.2 Sparse PATCH-FOOL & Mild PATCH-FOOL
논문에서는 더 다양한 분석을 위해서 basic attack 이외에도 두 variant attacks을 소개한다.
Sparse PATCH-FOOL
먼저 sparse PATCH-FOOL은 perturbation $E$의 sparsity를 조절한 version이다. 식은 다음과 같다.
$$argmax_{1 \le p \le n, \ E \in \mathbb{R}^{n \times d}, M \in \{0, 1 \}^{n \times d}} J(X+\mathbb{I}_p \odot (M \circ E), y) \ \ s.t. ||M||_0 \le k$$
기존 objective function에 M이 추가 되었는데, M은 predefine된 k개만큼 1을 가지고 나머지는 0인 binary mask이다. 이 M을 계산할 때 효과적인 학습을 위해 먼저 continuous values를 예측하고 가장 높은 top k개의 elements들을 1로 set하고 나머지는 0으로 만든다.
위 식을 통해 보고자 하는 바는 patch에 더해지는 perturbation의 sparsity를 한정해서 patch 내에서도 적은 pixels을 공격하였을 때의 결과는 어떨지를 보는 것이다.
Mild PATCH-FOOL
위 sparse PATCH-FOOL이 perturb되는 pixels의 수를 조절하는 것이었다면, Mild PATCH-FOOL은 perturbation의 크기를 조절하는 version이다. 논문에서는 $||E||_2 \le \epsilon$과 $||E||_{\infty} \le \epsilon$ 두 constraint에 대해서 실험을 한다.
3. Evaluatuion of PATCH-FOOL
PATCH-FOOL attack에 대한 여러 실험 결과들을 보여주는 section이다. 여다른 논문 리뷰 글과 비슷하게 결과와 간단한 정리만 할 것이다.
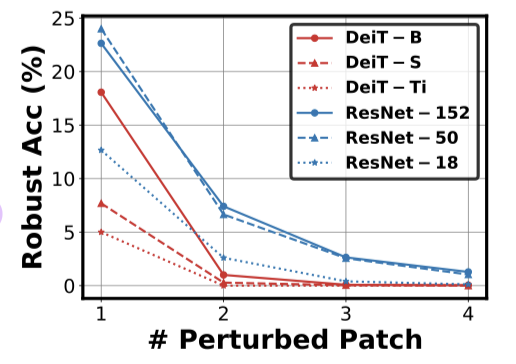
먼저 base PATCH-FOOL을 DeiT와 ResNet에 적용하였을 때의 결과이다. perturbed patch의 개수가 많아질 수록 accuracy가 줄어들고 잇고 거의 대부분의 경우 DeiT가 ResNet보다 vulnerable한 것을 볼 수 있다. 이는 이전 논문들의 결과 (ViT가 CNN보다 adversarial robustness가 높다)와 정반대의 결과이며, ViT 또한 어떻게 attack method를 만드는지에 따라서 CNN보다 약한 robustness를 가질 수 있다는 것을 보여준다.
Effectiveness of the Attention-aware Patch Selection
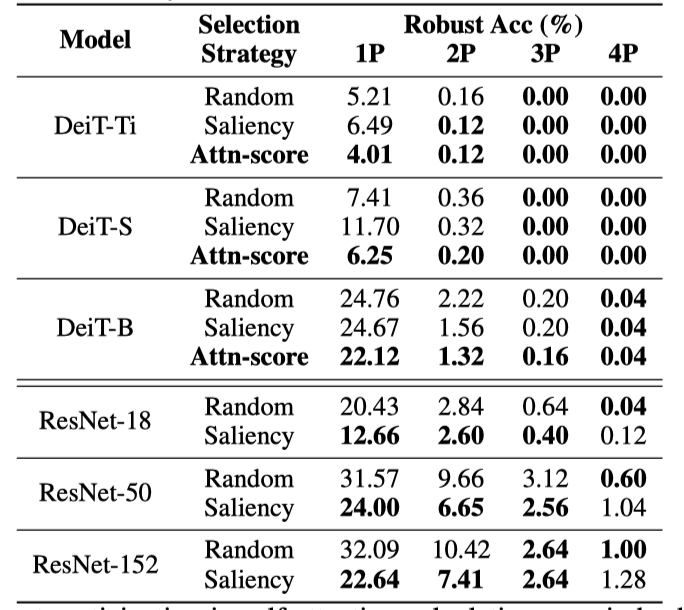
여러 patch selection methods들을 비교한 결과이다. 논문에서 고른 attention-score based method가 가장 좋은 결과를 보여준다. CNN은 해당 방법을 사용할 수 없기 때문에 saliency가 가장 좋은 방법이라 할 수 있다.
Effectiveness of the Attention-aware Loss
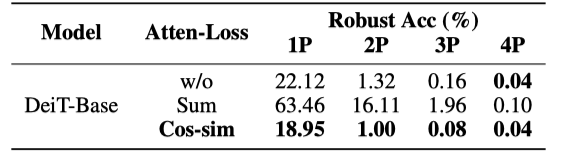
Attention-aware loss를 안주는 방식과 식 6번의 $\beta_t$를 0으로 주어 layerwise $J^{(l)}_{ATTN}$를 $J_{CE}$에 바로 sum하는 방식을 실험한 결과이며, 기존에 사용한 cosine-similarity (eq. 6)가 가장 좋은 결과를 내고 있다.
Benchmark against Sparse PATCH-FOOL
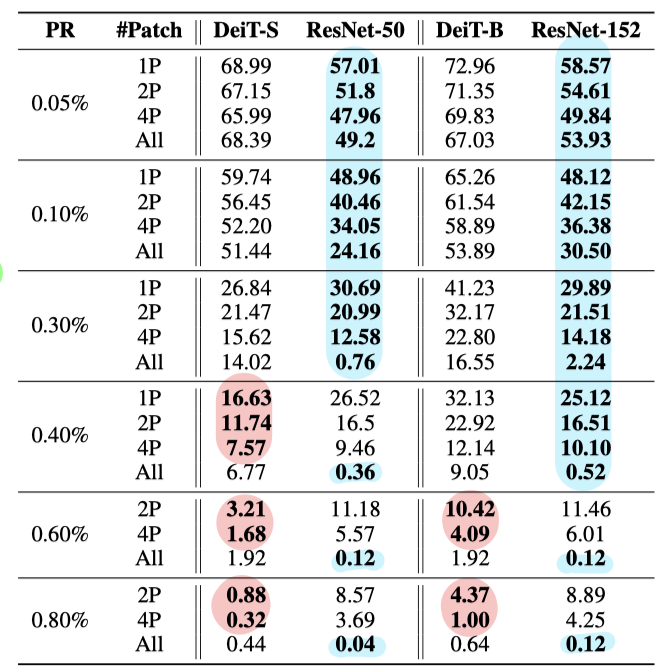
Sparse PATCH-FOOL을 하였을 때의 결과이며 여러 PR과 patch 개수에 대해서 실험을 한다. PR은 global perturabtion ratio로 $\frac{k}{total pixel}$을 나타낸다. 즉, PR이 높을 수록 sparsity가 낮아지는, patch 내 더 많은 픽셀을 공격하는 것이라 생각하면 된다.
CNN이 더 vulnerable한 경우를 파란색, ViT가 더 vulnerable한 경우를 빨간색으로 표시해두었고, 결과를 보면 perturbation의 sparsity가 높고 attack하는 patch의 개수가 많아질 경우 CNN이 취약함을 보였고, 그 반대의 경우 ViT가 취약성을 보였다.

위 table은 PR을 고정해놓고 공격하는 patch의 개수를 바꾸었을 때의 결과이다. PR이 낮을 경우에는 CNN이 모든 경우에 더 vulnerable하고 적당히 높은 경우에는 perturbed patch의 개수가 낮을 때 (1-16p) ViT가 더 vulnerable하다.
Benchmark against Mild PATCH-FOOL
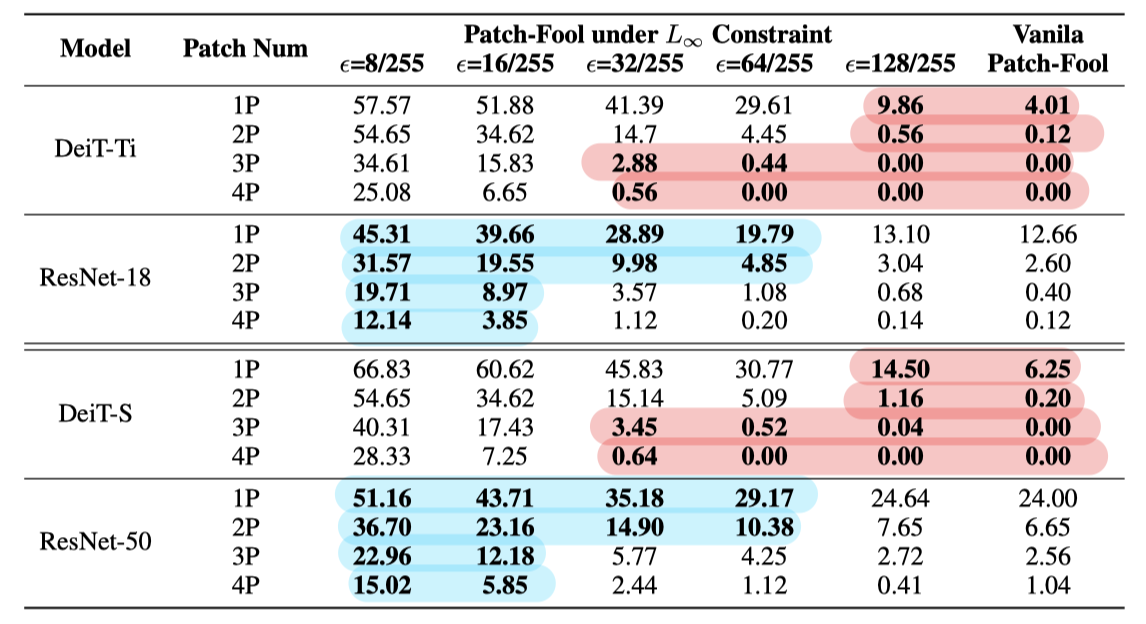
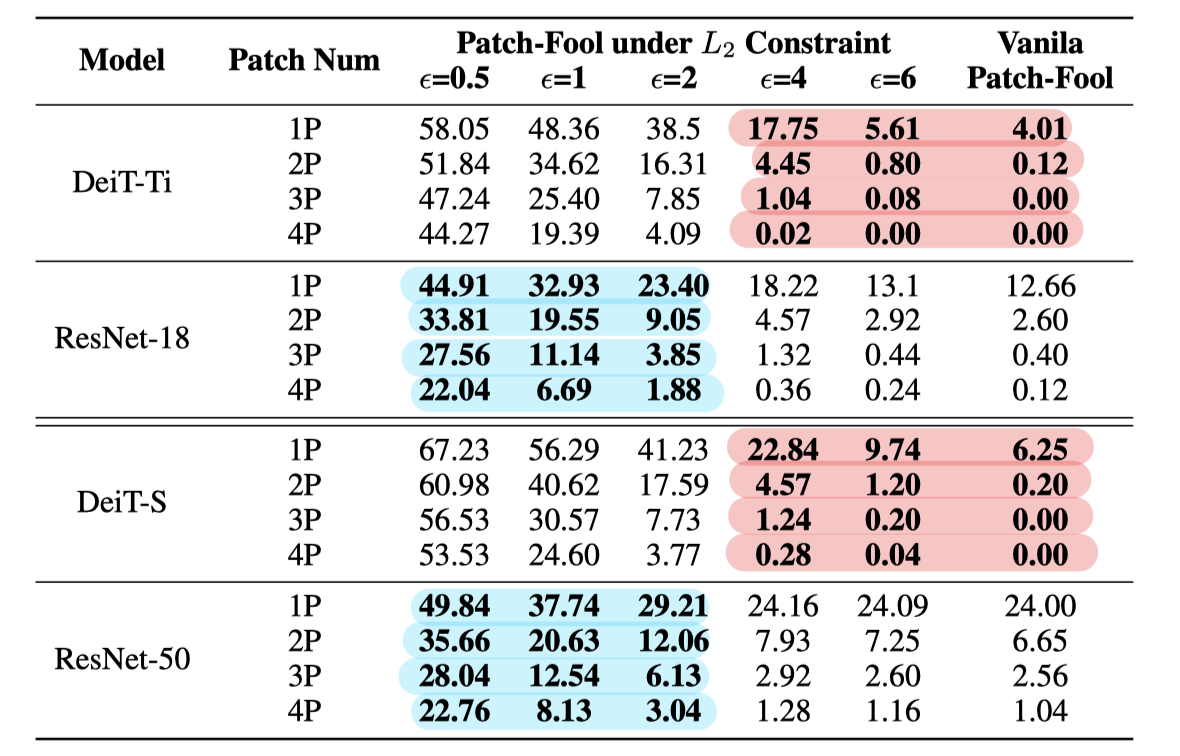
이번에는 Mild PATCH-FOOL에 대한 결과이다. 전반적으로 perturbation 크기가 클 수록 ViT가 더 vulnerable해지는 경향을 보인다.
'논문리뷰 > Adversarial Attack' 카테고리의 다른 글
| [논문 리뷰] Towards Evaluating the Robustness of Neural Networks(C&W Attack)(2) (0) | 2022.02.17 |
|---|---|
| [논문 리뷰] Towards Evaluating the Robustness of Neural Networks(C&W Attack)(1) (0) | 2022.02.12 |
| [논문리뷰] F-mixup: Attack CNNs From Fourier Perspective (2) | 2022.02.06 |
| [논문리뷰] Defensive Distillation (7) | 2022.02.05 |
| [논문리뷰] Defense-GAN (0) | 2022.01.28 |