2021. 5. 14. 18:34ㆍ인공지능/인공지능 기초
과적합은 머신러닝에서 많이 등장하는 문제 중 하나이다.
주로 데이터가 너무 적거나 모델이 과도하게 복잡한 경우에 발생하게 된다.

Over-Fitting(과적합)에 대해서 더 자세히 알아보도록 하자!
1. Over-Fitting(과적합)
과적합이란, train-set에 너무 과하게 모델이 최적화된 상태를 말한다.
모델이 over-fitting되면, train-set에서는 정확도가 매우 높게 나오지만 test-set에서는 낮은 정확도가 나온다. 한마디로 범용성이 없는 모델이 된다.
간단한게 Regression모델을 예로 들어보겠다.



이러한 문제를 완화시키기 위해서 다음과 같은 방법을 적용할 수 있다.
- 데이터를 추가 수집한다.
- feature의 개수를 줄인다.
- Regularization
- Early Stopping
- Model Averaging
- Dropout
1.1 데이터 추가 수집
제목 그대로 데이터를 추가로 수집하여 훈련을 시키는 것이다.
데이터의 양이 많고 다양할 수록 모델의 범용성은 더 높아진다.
만약 과소적합(under-fitting)이나 과대적합(over-fitting)이 일어났다면 데이터의 양을 늘리는 것이 가장 효과적이다.
하지만 데이터를 추가 수집하는 일은 쉬운 작업이 아니다..시간과 노력이 많이 필요하다..
1.2 Feature 축소
데이터를 설명하는 feature 중에는 관계성이 적거나 없는, 즉 쓸모없는 feature가 있을 수 있다.
이러한 feature는 모델의 학습에 악영향을 주며 Over-fitting을 일으킬 수 있다.
예를 들어, 주어진 데이터로부터 장미인지 해바라기인지를 판단하는 모델을 만든다 가정하자.

Feature는 다음과 같다.
- 가시의 여부
- 꽃의 색깔
- 개화 시기
- 잎의 개수
1, 2, 3번은 장미를 구분하는데 유효한 특징(feature)라는 것은 명확하다.
하지만 잎의 개수는 어떠할까?
잎의 개수가 장미를 표현하는 특징이 되기에는 애매하다....
이런 잎의 개수 같은 쓸모없는 또는 변별성(?)이 없는 특징들을 제거해줌으로써 Over-fitting 현상을 감소시킬 수 있다.
1.3 Regularization(정규화)
Regularization(정규화)는 모델의 일반화 성능을 높여 Over-fitting을 예방하는 방식이다.
모델을 표현하는 방정식에서 특정 가중치 파라메터(W)가 너무 큰 값을 가지게 되면 일반화 성능이 저하된다. 일반화 성능이 낮으면 학습 시, local noise에 의한 영향을 크게 받는다. 따라서 regularization으로, loss function에 일정 값(가중치(W)의 값)을 더해줌으로써, W 값이 클수록 가중치(W)가 줄어드는 폭이 커지게 학습을 시킨다.
**일반화 성능이 낮으면 local noise(특이점)의 영향을 많이 받는다.
**지금은 이해가 안될 수 있다. 아래에 더 자세히 설명할테니 일단 넘어가자.
1.3.1 Norm
먼저 Norm이라는 개념을 알아한다.
Norm이란, 벡터의 크기(길이)를 측정하는 방법으로, 두 벡터 사이의 거리를 측정하는 방법이기도 하다.
**여기서 p는 Norm의 차수를 의미한다. p=1이면 L1 Norm, p=2이면 L2 Norm.
L1 Norm
L2 Norm
L1과 L2 Norm의 차이

L1 Norm은 빨강, 파랑, 노랑 선으로 표현 될 수 있지만, L2 Norm은 오직 초록색 선으로만 표현된다.
즉, L1 Norm은 여러 path를 가지지만, L2 Norm은 오직 unique shortest path만을 가진다.
1.3.2 Loss
이번엔 위에서 배운 L1 Norm과 L2 Norm으로 만들어진 L1 Loss와 L2 Loss에 대해서 살펴보겠다.
L1 Loss
**여기서
L2 Loss
L1과 L2 Loss의 차이
| L2 Loss Function | L1 Loss Function |
| Not very robust | Robust |
| 안정된 Solution | 불안정한 Solution |
| unique한 Solution | 다수의 Solution이 나올 수 있음. |
직관적으로 보았을 때, L2 loss가 오차의 제곱을 더하기 때문에, 외부 값에 더 큰 영향을 받는다.
또한, L2는 unique한 해를 내지만, L1은 경우에 따라 특정 feature없이도 같은 해를 도출 할 수 있다.
예를 들어보자
a=(0.3, -0.3, 0.4), b=(0.5, -0.5, 0)이라 할 때, L1 Norm과 L2 Norm을 구해보자
L1 Norm:
L2 Norm:
즉, L1 Norm은 feature selection이 가능하고, 이 특징은 L1 Regularization에 동일하게 적용된다.
1.3.3 Regularization(정규화)
Regularizaiton에서 가중치를 더할 때, L1 또는 L2 Norm을 사용할 수 있다.
**또는 둘 다 사용하는 방법도 있다.
다음 식은 L2 Norm을 사용한 정규화 식이다.
**여기서
식에서 알 수 있듯이,
만약
**보통 0.1만 주어도 가중치를 높게 준다는 뜻이다.
기존 cost function에 가중치의 크기가 더해지면서, 특정 가중치가 커지는 것을 예방한다.
예를 들어 더 자세히 살펴보자.
만약 n번째의 가중치 파라메터
우리가 지난 번에 배운 바에 의하면 학습할 때 Cost Function의 결과 값을 낮추는 방향으로 진행한다고 배웠다. 즉,
반대로
1.3.4 다른 역할의 Regularization
위에서 Regularization이 하는 역할 중 하나를 배웠다. 이번에는 Regularization이 할 수 있는 또 다른 역할에 대해서 알아보겠다.
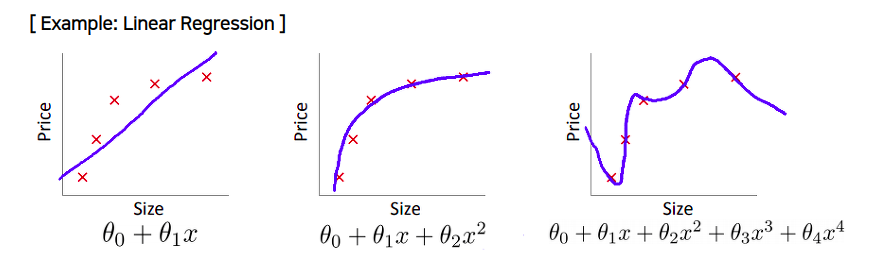
출처: andrew ng machine learning lecture
위 이미지 예를 살펴보자. 파라메터의 개수가 많아질 수록 모델이 점차 복잡해지고 결국에는 오버피팅이 일어나는 것을 알 수 있다.
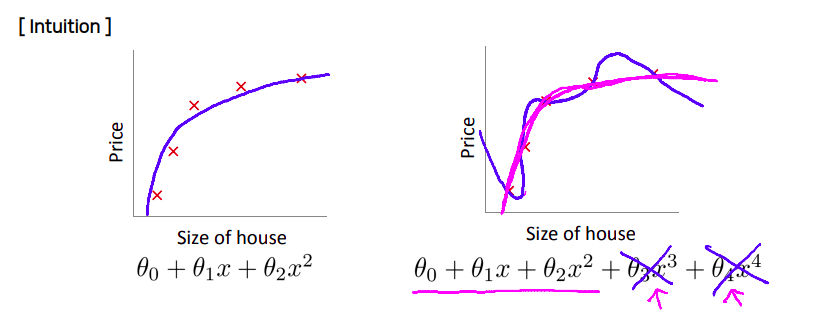
출처: andrew ng machine learning lecture
Regularization은 큰 w에 대해서는 더 큰 폭으로 가중치 파라메터를 감소시키지만, 전체적으로 모든 w(가중치)값이 줄어들게 된다. 이로 인해 모델이 좀 더 단순하고, smooth해지면서 Over-fitting을 방지하게 된다.
1.4 DropOut
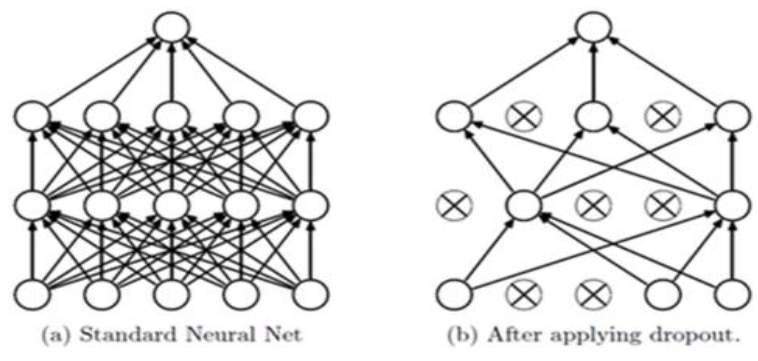
Dropout이란, Neural Network에서 전체 노드를 사용하는 것이 아니라 random으로 일부 노드를 배제하고 학습을 하는 것을 말한다. Dropout은 regularizer와 같이 특정한 노드의 가중치가 크게 학습되는 것을 방지함으로써 일반화 능력의 저하를 방지하는 역할을 한다.
단, Over-fitting을 방지하기 위한 방법이므로 train-set에만 적용되고, test-set을 predict할 때는 사용되지 않는다.
1.4.1 DropOut의 효과
DropOut의 효과를 더 자세히 살펴보자!
Voting 효과
일정한 mini-batch구간에서 Dropout에 의해 줄어든 신경망을 이용해 학습을 하게 되면,
그 신경망은 그 구간에서 fitting이 되고, 또 다른 미니배치 구간에서 학습된 신경망은 마찬가지로
또 그 구간에서 fitting이 되기 때문에, 이런 과정을 반복하게 되면 voting에 의한 평균 효과를 얻을 수 있다.
Co-adaption을 피하는 효과
특정 노드의 바이어스(B)나 가중치(W)가 큰 값을 갖게 되면, 그것의 영향이 커져서 다른 뉴런들의 학습 속도가 느려지거나 학습이 제대로 진행되지 못할 수 있다.
Dropout은 어떤 특정 노드의 가중치나 바이어스가 크게 영향을 주지 못하게 만들기 때문에 노드들이 서로 동조화(co-adaption)하는 것을 피할 수 있다.
이렇게 Over-fitting과 그 해결법에 대해서 간단히 알아보았다.
Over-fitting은 머신러닝 학습에서 많이 등장하는 문제이기 때문에 여러가지 보완법이 계속해서 나오고 있다.
이러한 보완법들은 말그대로 어느정도 서포트를 해주는 것이지 over-fitting자체를 완전하게 해결하는 방법은 아직 존재하지 않는다. 하지만 충분한 데이터셋을 가지고 학습하였는데 over-fitting 문제가 발생하였다면 위의 보완법들을 사용해 어느정도 효과를 볼 수 있을 것이다.
'인공지능 > 인공지능 기초' 카테고리의 다른 글
| [인공지능 기초] 6. ANN(Artificial Neural Network) (0) | 2021.10.10 |
|---|---|
| [인공지능 기초] 5. 퍼셉트론 (0) | 2021.07.06 |
| [인공지능 기초] 4. 신경망 학습 (0) | 2021.05.25 |
| [인공지능 기초] 2. 학습과 데이터 (0) | 2021.05.13 |
| [인공지능 기초] 1. Basic Machine Learning (0) | 2021.05.08 |