[논문 리뷰] Matching Networks for one shot learning
1. Introduction

사람은 새로운 개념을 배울 때 아주 적은 수의 데이터로도 object에 대해 generalize하는 것이 가능하다. 하지만 CNN은 어떠한가? 위의 기린이라는 새로운 object를 학습하려면 많은 이미지를 필요로 한다. 이미지 데이터와 그 label을 만드는 것은 간단하게 생각해보아도 비용이 매우 비쌀 것이다.
"few-shot learning"은 Neural Network도, 사람과 같이, 새로운 개념을 배울 때 아주 적은 데이터로도 잘 학습할 수 있도록 만드는 것을 목표로 한다.

출처: https://nanonets.com/blog/data-augmentation-how-to-use-deep-learning-when-you-have-limited-data-part-2/
large datasets을 필요로 하는 딥러닝의 문제를 회피하기 위한 대표적인 예로 Data augmentation과 regularization이 있다. 이는 적은 데이터를 사용할 때, 어느 정도의 over-fitting을 완화시켜주지만 좋은 성능을 내기에는 부족하다.
또한 논문에서는 parametric model을 사용하기 때문에 learning 속도가 느리다는 점을 지적한다. 반대로 non-parametric models(ex. nearest negihbors)는 training할 필요가 없어 위와 같은 문제를 해결하지만 metric에 따라서 성능이 바뀐다는 문제가 있다. 저자들은 이러한 parametric과 non-parametric models의 문제는 해결하고 장점만 사용하도록 노력을 기울인다.
2. Model
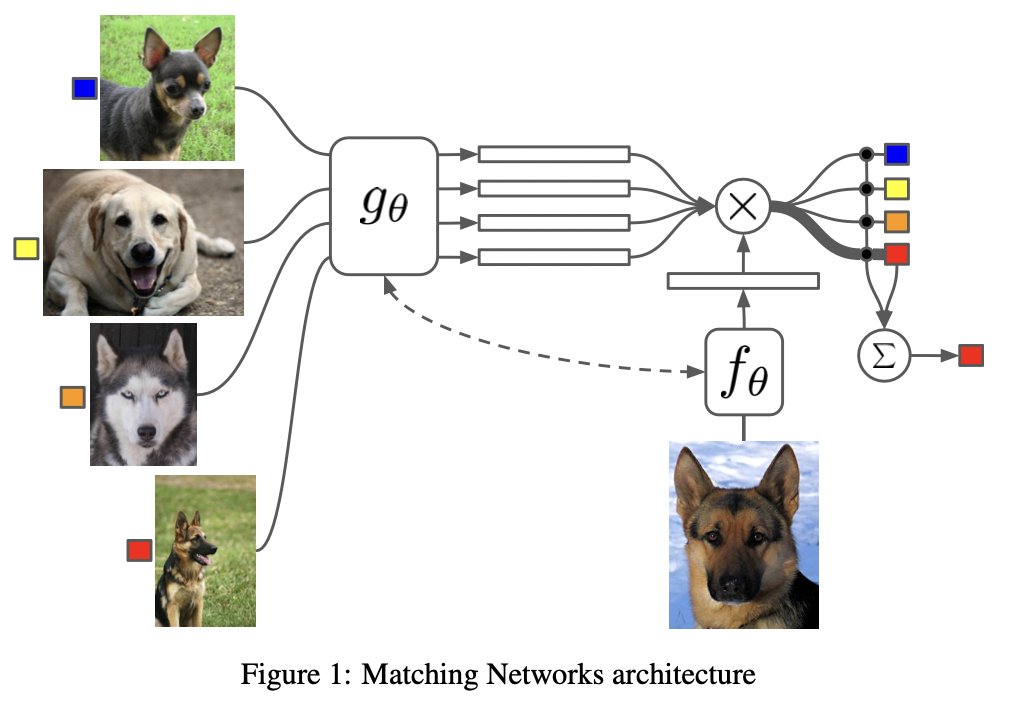
2.1 Model Architecture
저자들은 one-shot learning을 풀기 위해서 non-parametric approach를 사용한다. 위 이미지가 "matching network가 어떻게 동작하는지" 잘 설명하고 있으므로 자세히 살펴보자!
먼저 위 예제는 4 way 1 shot learning이다. 즉, 4가지의 클래스가 있고 각 클래스당 1개의 이미지만을 사용하였다.
matching network이란 결국 attention mechanism을 통해서 4개의 support set과 1개의 batch set과의 similarity를 구하고 argmax를 취해 가장 similarity가 높은 클래스를 batch image의 label로 주는 것이 목표이다. 이를 식으로 나타내면 다음과 같다.
$$\hat{y} = \sum^k_{i=1} a(\hat{x}, x_i)y_i$$
** $\hat{x}$는 batch image, $x_i$는 support image, a()는 attention kernel이다.
>> attention kernel의 output이 probability distribution이 되므로 위 식을 "kernel desity estimation"으로 해석할 수도 있고, 또는 $\hat{x}$가 $x_i$와 b만큼 떨어져 있을 경우 0, 그 외에는 어떠한 상수 값을 가질 때 이를 "'k-b' nearest-neighbours"로써 바라볼 수도 있다.
The attention kernel
위 식에서 a()에 해당하는 부분으로 attention mechanism에 해당한다. 논문에서는 방법으로 softmax와 cosine distance의 조합을 사용한다. 이를 식으로 나타내면,
$$a(\hat{x}, x_i) = e^{c(f(\hat{x}), g(x_i))} / \sum^k_{j=1} e^{c(f(\hat{x}), g(x_j))}$$
>> f()와 g()는 embedding function으로 "vgg"나 "inception"과 같은 pretrained network를 사용하거나 새로운 network를 학습해서 사용할 수도 있다. 또한, f()와 g()는 같을 수 있다.
Full context embeddings
attention kernel에서 support set $x_i$을 g함수를 통해서 embedding할 때, support set의 다른 input값들의 정보는 고려하지 않게 된다. 따라서 논문에서는 이를 $g(x_i, S)$로 바꾸어 모든 support set의 정보를 더하여 embedding을 하도록 한다. 이 때 논문에서는 sequence 정보를 양방향으로 고려하기 위해서 bidirectional LSTM을 사용한다.
>> 이는 만약 $x_j$가 $x_i$와 매우 비슷할 때 embedding 또한 비슷해지도록 만들어준다.
두번째로 $\hat{x}$를 f함수를 통해서 embedding할 때 support set S를 고려하기 위해서 $attLSTM(f'(x), g(S), K)$를 사용한다. f'(x)는 VGG와 같은 pretrained model을 사용해서 나온 feature이고, K는 LSTM의 개수, g(S)는 위에서 이야기한 bidirectional LSTM의 output이 된다.
>> 이는 잠재적으로 모델이 support set S의 일부 요소들을 무시할 수 있게 만들고, attention을 계산할 때 depth를 더해주는 역할을 한다.
2.2 Training Strategy
이제 이 Matching Network를 실제로 어떻게 학습시키는지 살펴보자. 먼저 일반적인 딥러닝 학습은 batch learning을 하게 되는데, few-shot learning의 경우 이러한 학습 방식에 잘 동작하지 않는다고 한다. 따라서 저자들은 test time에서의 inference와 training procedure를 가능한 맞출 수 있는 "episode learning"을 제안한다. 이를 먼저 식으로 살펴보면 다음과 같다.
$$ \theta = argmax_{\theta} E_{L\~T} [E_{S\~L, B\~L}[\sum_{(x,y) \in B} logP_{\theta}(y|x, S)]]$$
천천히 순서대로 살펴보면, 먼저 task T에서 L을 sampling한다. 여기서 T는 적은 unique classes(ex. 5)와 적은 class 당 이미지 수(ex,up to 5)를 가지는 데이터셋이 되고, L은 이 T가 가진 클래스들 중에서 random으로 정해진 개수만큼 뽑아서 가져오게 된다. 그 다음 sampling된 L로부터 support set과 batch set을 sampling한다. 그리고 이렇게 만들어진 support set과 batch set을 input으로 위에서 설명했던 matching network를 적용하여 batch 이미지의 label을 예측하고 그 error가 minimize되도록 학습하게 된다. 이러한 과정이 1 episode가 되고, 다음 epsiode에서 다시 random으로 sampling이 진행되고 똑같은 방식으로 error를 minimize한다.
>> 여기서 $\theta$는 embedding function f()와 g() 모델에 대한 parameter 이다.
Example
이렇게 글로만 보면 이해가 어려울 수 있으니 예를 통해서 알아보자!

다음과 같이 5개의 클래스와 클래스당 5장의 이미지를 가지는 데이터셋 T가 있다고 하자. 이제 T에서 L을 sampling하는데 여기서는 2개의 클래스를 랜덤으로 고를 것이다.

이번 episode에서는 "dog"와 "lion" 두 클래스가 뽑혔다고 하자. 이제 sampling된 L에서 support set S와 batch set B를 random sample한다. 예에서는 support set 4장과 batch set 1장으로 나눌 것이다. 마지막으로 support set과 batch set을 input으로 matching network를 통해 batch set에 대한 label을 잘 예측하도록 학습시키면 된다.
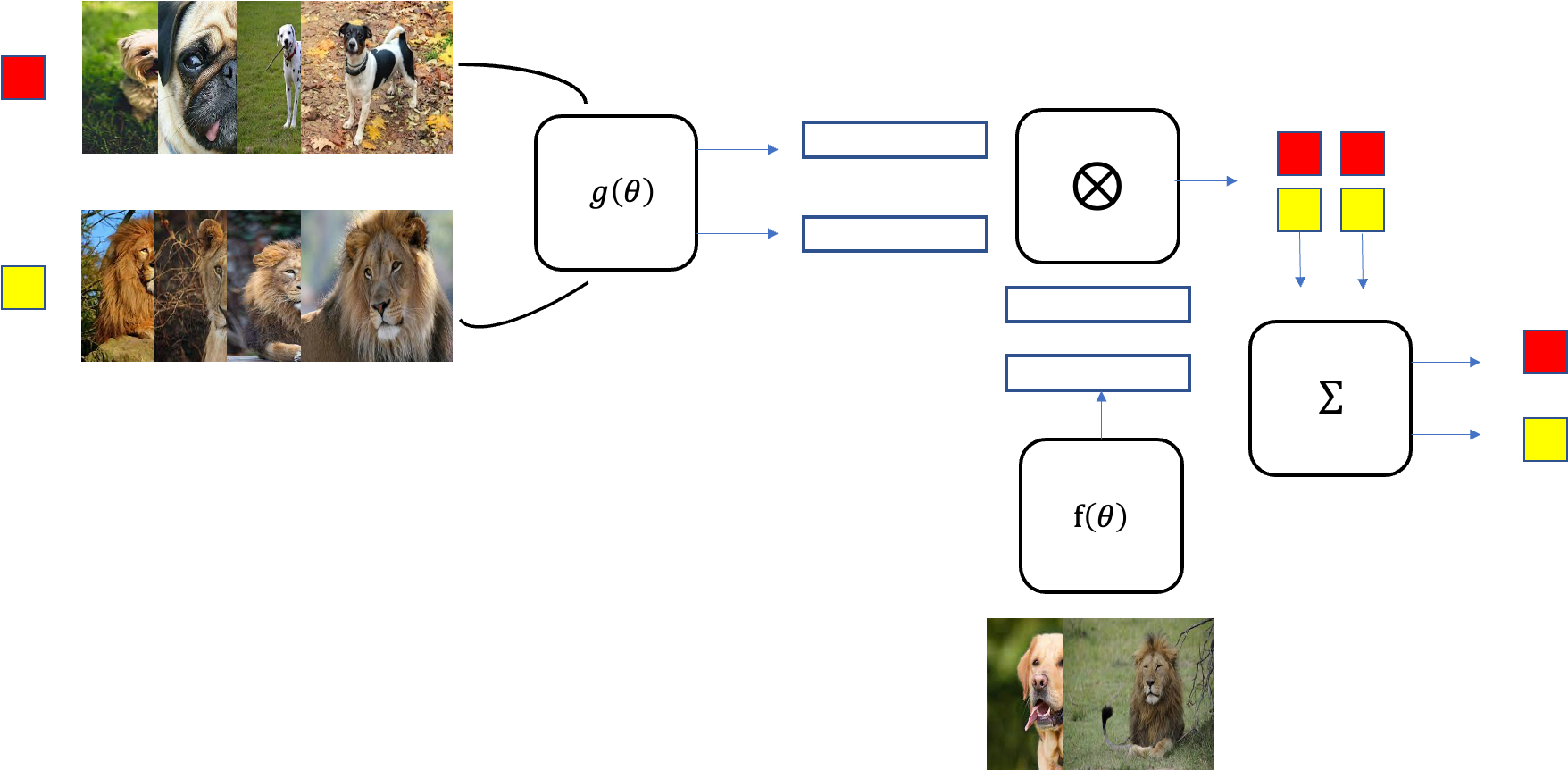
이렇게 한 episode가 끝난 것이고 이를 정해둔 episode만큼 반복하게 된다. epsiode마다 샘플링되는 두 개의 클래스와 그 클래스들의 이미지 데이터셋으로부터 샘플링되는 support set S와 batch set B는 random이기 때문에 epsiode마다 다른 조합으로 학습이 될 것이다. 모든 episode가 끝나고 학습이 되었다면 training 데이터셋에 없었던 새로운 이미지셋으로 batch set의 label을 예측하여 테스트를 하게 된다.
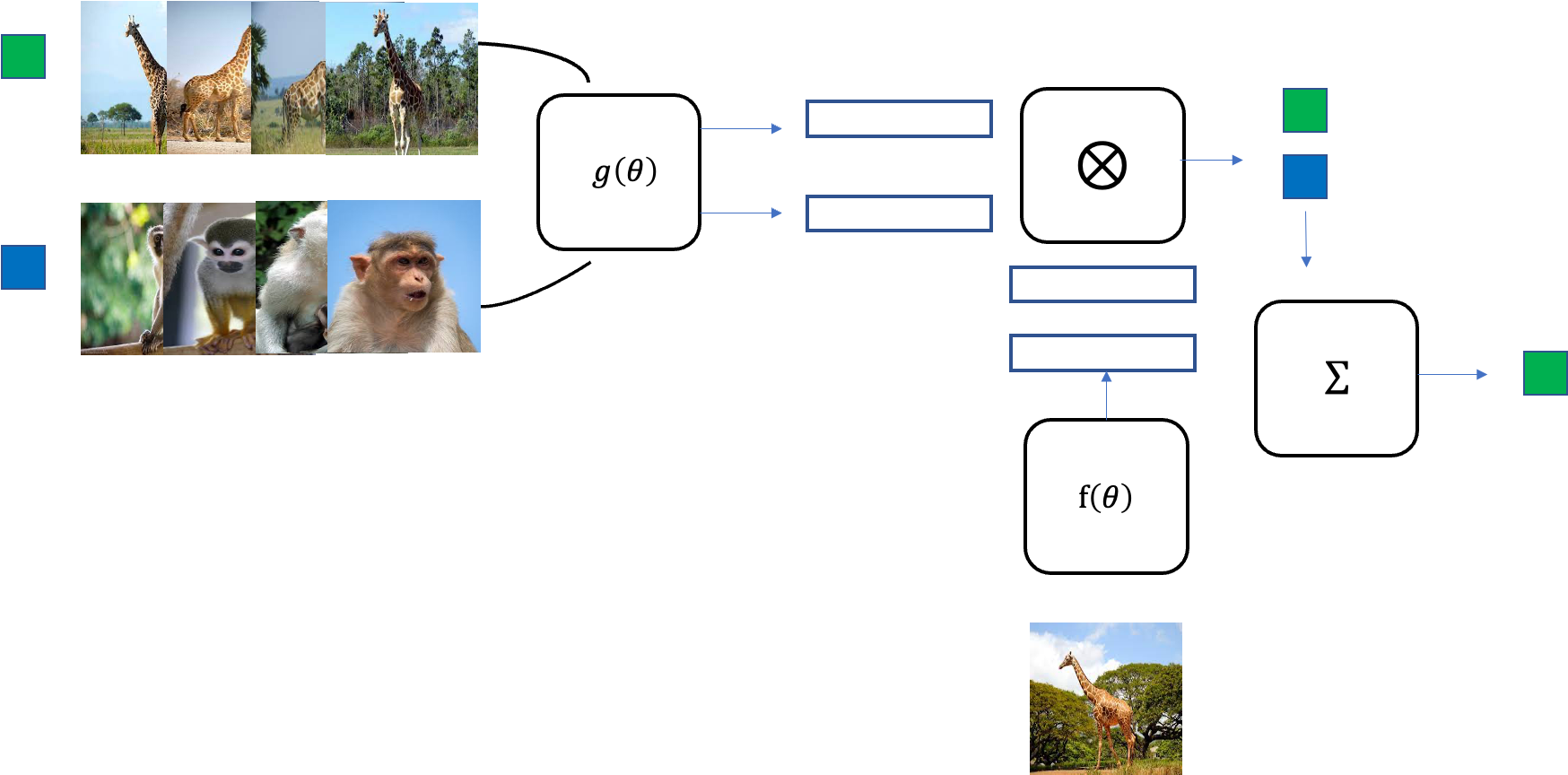
만약 학습이 잘되었다면 training에서 사용하지 않았던 원숭이와 기린 이미지에 대해서도 알맞은 label을 예측할 수 있을 것이다. 이처럼 Matching network에 좋은 점은 새로운 데이터셋에 대해서 다시 fine-tuning을 해줄 필요가 없다는 점이다.
3. Experiments
논문에서는 3종류의 데이터셋을 사용하여 matching network를 실험하였다. 자세한 설정은 논문을 참고하길 바라고 여기서는 간단히 실험 결과에 대해서만 리뷰하겠다.
3.1 Image Classification Results
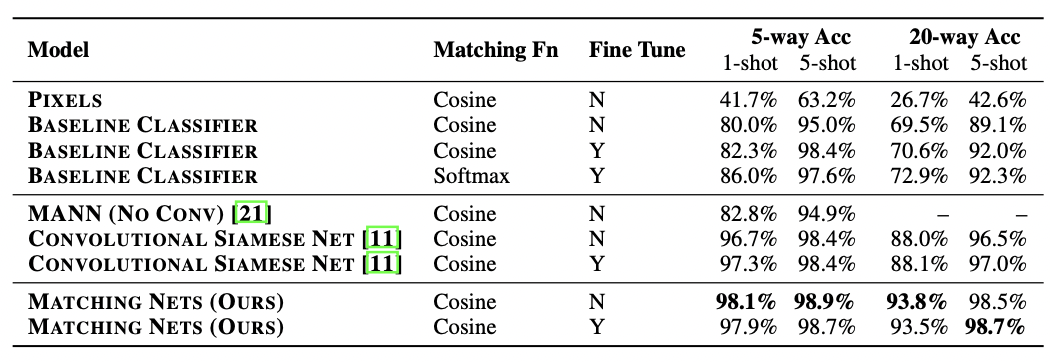
먼저 image classification task에 적용한 실험이다. baseline(state-of-the-art classifier, Inception based)과 다른 few-shot learning methods인 MANN과 Siamese net과 Matching Net의 성능을 비교하며 보여주고 있다. Matching Network가 다른 methods보다 5-way, 20-way의 1-shot, 5-shot 모두 outperform한 성능을 보여주고 있고, 추가로 support set S'(unseen support set)을 fine tuning하였을 때 성능이 향상된 것을 알 수 있다.
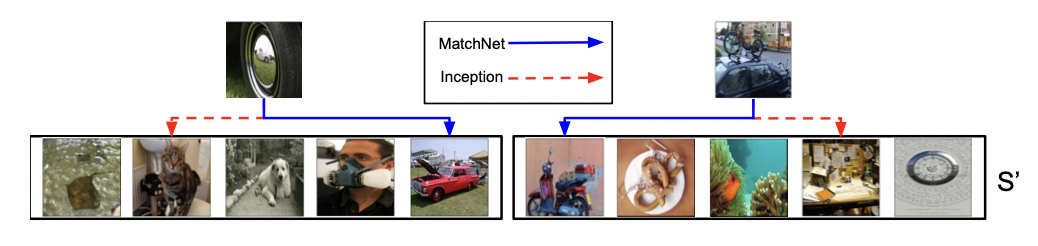
밑의 그림은 baseline classifier보다 MatchNet이 더 prediction을 잘한다는 것을 qualitatively 보여준다.
Mini Imagenet datasets

먼저 imageNet이 실험을 할 때 드는 resources가 너무 많기 때문에 저자들은 이를 조정하여 새롭게 miniImageNet이라는 데이터셋을 제공하였다. 이는 100개의 classes와 class당 600장의 84x84x3크기의 이미지로 이루어져있다.
여기서 저자들은 재밌는 실험을 하였는데, training set으로부터 random으로 118개의 클래스를 제외하고 이 제외된 118개의 클래스들에 대한 test를 진행하는 "$L_{rand}$" setup과, dog 종류에 해당하는 118개의 클래스를 제외하고 non-dog 클래스들만 학습시킨 후에 제외된 dog 클래스 데이터를 test로 사용하는 "$L_{dogs}$" setup을 진행하였다. 이에 대한 결과는 위 Table 3에서 볼 수 있다. $L_{rand}$의 경우 matching nets이 unseen 데이터에 대해서도 매우 좋은 성능을 보이지만, $L_{dogs}$는 그렇지 못한 것을 알 수 있다. 저자들은 이러한 원인으로 training에서는 $\neq L_{dogs}$로부터 random sampling된 데이터를 사용하는데 반해 $L_{dog}$의 경우 클래스들 간 이미지들이 서로 비슷하기 때문에 분류가 어려웠을 것이라 보고 있다.
추가로 Language modeling에서도 Matching network를 사용한 실험이 있는데 이는 생략하도록 하겠다. 또한 사용된 embedding fuctnion f()와 g()에 대한 model description은 논문의 appendix에 설명되어있으므로 원하면 읽어보길 바란다.