[인공지능 기초] 8. Convolutional Neural Networks(CNN)
기존 Deep Neural Network의 문제점
왜 이전의 DNN을 사용하지 않고 굳이 CNN이라는 새로운 개념을 만들어냈을까? 어떤 문제가 있는지 살펴보자.

고차원 input 데이터
먼저 input 이미지가 매우 고차원이다. 사람이 불편하지 않게 볼 수 있는 사이즈가 대략 256x256인데 color이미지면 차원만 256x256x3=196608이된다. 여기다 hidden layer를 추가하면 어떻게 될까? layer가 늘어날 때마다 parameter의 수가 기하급수적으로 늘어날 것이다. 이러한 문제로 인해 엄청난 계산량을 필요로 하고, 모델의 complexity도 높아져 overfitting이 일어날 수 있게 된다.
Flexibility of Topology
DNN은 1차원 벡터만을 사용할 수 있기 때문에 이미지를 flatten해야만 한다. 여기서 먼저 이미지의 spatial한 정보를 많이 잃게 되고, 모든 노드와의 connection을 사용하면서 weight도 각 각 다르기 때문에 이미지 픽셀 간의 연관성 정보를 거의 담지 못하게 된다. 이러한 이유로 topology 변화에 sensitive해지는 문제가 발생한다. 간단하게 말해서 이미지가 조금만 바뀌더라도(ex. rotation, transition) 그 데이터를 다시 학습해주어야 한다는 것을 의미한다.
CNN(Convolution Neural Network)

CNN은 주로 이미지 관련 task에 많이 사용된다. 위에서 설명했듯이 DNN은 input이 1차원이어야하기 때문에 다차원인 이미지를 1차원 벡터로 flatten해주어야 한다. 이로 인해 이미지의 spatial 정보를 거의 잃게 되고 이로 인해 generalize한 train이 제대로 이루어지지 않게 된다. 이러한 문제를 해결하기 위해 나온 히어로가 CNN님이시다.
Receptive Field

formal하게 말하면 외부 자극이 전체에 영향을 끼치는 것이 아니라 특정 영역에만 영향을 준다는 의미이다. 좀 더 이미지에 빗대어 말하면 특정 위치에 있는 픽셀은 그 주변에 있는 픽셀들과의 상관관계가 높고 거리가 멀어질 수록 관계성이 떨어진다는 것이다. 직관적으로 생각해봐도 위 이미지를 예로 들 때, 동공의 한 픽셀은 그 주변 픽셀(동공 주위)들과 가장 연관도가 높을 것이고 먼 픽셀(배경)과는 낮은 연관성을 가질 것이다.
따라서 이미지 전체 영역에 대해서 서로 동일한 중요도로 처리하는 대신에, 특정 범위로 한정하여 처리를 하면 더 효과적일 것이라는 아이디어이다.
CNN의 특징
첫번째로 CNN은 locality 특성을 가지고 있다. receptive field와 유사하게 local 정보를 활용하는데, 공간적으로 인접한 신호들에 대한 상관관계를 비선형 필터를 적용해 추출해 낸다.
**어렵게 들리지만 결국 Convolution 후에 non-linear activate function을 적용하는 것을 뜻한다.
이런 필터를 여러 개 적용하면 다양한 local 특징을 추출해 낼 수 있고, convolution과 subsampling을 거치면서 local feature에 대한 필터 연산을 반복적으로 적용해 점진적으로 global feature를 얻게 된다.
두번째로 CNN은 가중치를 공유하는 특징을 가진다. 동일한 계수를 갖는 filter를 전체 이미지에 반복적으로 적용함으로써 파라메터의 수를 줄이고, topology 변화에 robust하도록 학습이 된다.
Convolution layer

filter를 이용하여 특징을 추출해내는 과정이다. 이는 이미지의 정보를 최대한 보존하면서 semantic한 1차 벡터를 만들 수 있게 해준다.
위에서 말했듯이 filter는 공용 파라메터를 가지며 이미지의 모든 영역에 적용된다. CNN에서의 학습은 이 filter의 파라메터를 update시키는 것이라고 생각하면 된다. filter의 size는 hyper-parameter인데 보통 3x3을 많이 사용한다. 큰 filter size를 하나 사용하는 것과 작은 filter size를 여러 개 사용하는 것에 대한 논란은 여전히 많은데 초반 layer에는 큰 filter size, 후반으로 갈 수록 작은 layer를 사용하는 것이 일반적이다.
또한 filter의 개수는 hidden layer의 node 수와 비슷한 개념이라고 생각하면 되고, 개수가 많을 수록 그만큼 다양한 filter를 찾을 수가 있지만 필요한 계산량과 메모리가 많아지게 된다. 보통 초반 layer에는 많은 filter를 쓰고 후반으로 갈수록 그 수를 줄여나간다.
Strides

출처: https://developersbreach.com/convolution-neural-network-deep-learning/
또 다른 hyper-parameter로 stride가 있다. stride란 filter를 몇 픽셀씩 이동하면서 적용할 것인지를 정하는 파라메터이다. 위 예에서 왼쪽은 stride=1이므로 한칸씩 이동하는 것을 볼 수 있고, 오른쪽은 stride=2로 2칸씩 이동하게 된다.
stride를 크게 주면 그만큼 output의 크기가 작아지기 때문에 보통 연산량을 줄이기 위한 목적으로 사용된다. 같은 역할을 하는 pooling과 어느 쪽이 좋은지 논란이 있지만 최근에는 stride=2를 더 많이 쓰는 추세이다.
Padding
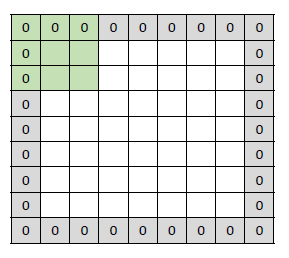
그냥 convolution을 적용하게 되면 주변 픽셀과 함께 연산을 하는 특성상 경계면은 계산을 할 수 없게 된다. 이러한 경계면 정보를 살리기 위하여 주위 픽셀을 0으로 채워주는 것을 padding이라고 한다.
Output size 계산
가끔 Network를 코딩하거나 논문을 볼 때, output size를 알아야하는 경우가 있다. 입력 크기를 (H, W), 필터 크기를 (FH, FW), 출력 크기를 (OH, OW), 패딩을 P, Stride를 S라 하면 계산식은 다음과 같다.
$$OH=\frac{H+2P-FH}{S}+1, \ \ OW=\frac{W+2P-FW}{S}+1$$
Pooling layer

pooling은 stride와 같이 output의 크기를 줄여주는 역할을 한다. 종류도 여러가지가 있는데 주로 사용되는 것은 Max pooling과 Average Pooling이다. 예에서 볼 수 있듯이, max pool은 filter에서 가장 큰 값을 뽑아내어 사용하는 기법이고 average pool은 그 평균을 사용하는 기법이다.
**pooling은 보통 parameter가 없다. 즉, 학습하는 Layer가 아니다.