[논문리뷰] Amplitude-Phase Recombination
요즘 딥러닝과 forier domain 사이의 관계 또는 조합 관련하여 논문을 읽고 있는데, 그 중 흥미로운 논문 하나를 리뷰하려고한다.
https://arxiv.org/abs/2108.08487
Amplitude-Phase Recombination: Rethinking Robustness of Convolutional Neural Networks in Frequency Domain
Recently, the generalization behavior of Convolutional Neural Networks (CNN) is gradually transparent through explanation techniques with the frequency components decomposition. However, the importance of the phase spectrum of the image for a robust vision
arxiv.org
먼저 이 논문을 읽기 전에 사전 지식으로 fourier transform을 알아야 하는데, 갓크 프로그래머님께서 아주 잘 설명해놓으셨으니 이 글을 참고하면 좋을 것 같다.
https://darkpgmr.tistory.com/171
Fourier Transform(푸리에 변환)의 이해와 활용
푸리에 변환(Fourier transform)에 대해서는 예전부터 한번 정리를 해야겠다고 생각만 했었는데 이번에 기회가 되어 글을 올립니다. 푸리에 변환(Fourier transform)은 신호처리, 음성, 통신 분야에서 뿐만
darkpgmr.tistory.com

1. Unintuitive Generalization Behavior
비전 분야에서 딥러닝이 등장하고 나서 매우 큰 발전이 이루어졌다는 것은 아무도 반론할 수 없을 것이다. 최근의 딥러닝의 성능은 인간의 인지 능력과 같거나 그보다 뛰어날 정도이다.
하지만 딥러닝이 black-box인만큼 어떠한 현상이나 문제가 일어났을 때, 이를 설명하거나 분석하기가 매우 어렵다는 문제가 있다. 이 논문에서는 CNN에서 발생할 수 있는 이해하기 어려운 현상들을 크게 3가지로 분류하고 있다.
- Adversarial Attack
- Common Corruptions
- Overconfidence of out-of-distribution
Adversarial Attack

Explaining and Harnessing Adversarial Examples paper
먼저 adversarial attack이란, 원래의 이미지에 아주 작은(사람의 눈으로 인지할 수 없을정도로) perturbation을 가함으로써 딥러닝의 성능을 크게 떨어트리는 것을 말한다.
위의 예를 보면, 딥러닝 모델이 판다 이미지를 57.7%의 확률로 판다라고 잘 예측을 하였는데, perturbation을 섞은 오른쪽 이미지는 사람 눈으로 보았을 때는 아무리 보아도 판다이지만 모델은 이를 무려 99%의 확률로 gibbon(긴팔원숭이)라 예측하는 것을 알 수 있다.
Common Corruption

Benchmarking neural network robustness to common corruptions and perturbations paper
common corruption은 좀 더 generalize한 corruption인데, 대표적인 것들로는 noise, blur 등이 있겠다.
이러한 작은 변화(real-world에서 발생할 수 있는)에도 딥러닝 모델의 성능은 좌지우지 된다.
Overconfidence out-of-distribution
먼저 out-of-distribution data란, train-set에 포함되지 않는 class or label을 가지는 데이터를 말한다. 일반적으로 생각했을 때, 이러한 데이터는 모든 class에 작은 convidence를 가져야하지만 딥러닝 모델은 이를 매우 큰 confidence로 예측하는 경향을 보인다.
이러한 Neural Network의 unintuitive generalization behavior를 분석 및 해석하기 위해 많은 사람들이 여러 관점에서 연구를 하였고, 그중 하나가 frequency domain에서의 관점이고 이 논문에서도 이러한 관점으로 분석을 하고 있다.
2. Generalizability of CNN in Frequency domain

Amplitude-Phase Recombination paper
여러 연구가 진행되면서 밝혀진 몇가지 사실들이 있는데, 먼저 Convolutional Neural Network(CNN)은 high-frequency image component로부터 많은 정보를 catch한다는 것이다. 물론 이 말이 low frequency component로부터 아무 정보도 얻지 않는다는 말은 아니다.
두번째로는 fourier domain에서 amplitude spectrum의 변화에 예민하다는 사실이다. 이 논문에서는 amplitude가 noise나 common corruption에 영향을 받기 쉬운, unrobustness한 특성이라 주장하고 그렇기 때문에 CNN의 prediction performance도 저하될 수 있다 말한다.
Out-of-distribution data에 대해서는, in-of-distribution data와 전혀 다른 이미지 분포를 가지지만 고주파 amplitude 성분에서 어떠한 similarities가 있기 때문에 CNN이 제대로 구별하기 어렵다고 한다.
그런데 이러한 딥러닝과 반대로, 사람의 visual system은 robustness한 object 인지를 위해서 amplitude가 아닌 phase 정보를 더 집중해서 본다는 사실이다. 위의 그림은 이러한 딥러닝과 사람의 vision system과의 차이를 보여주고 있다.
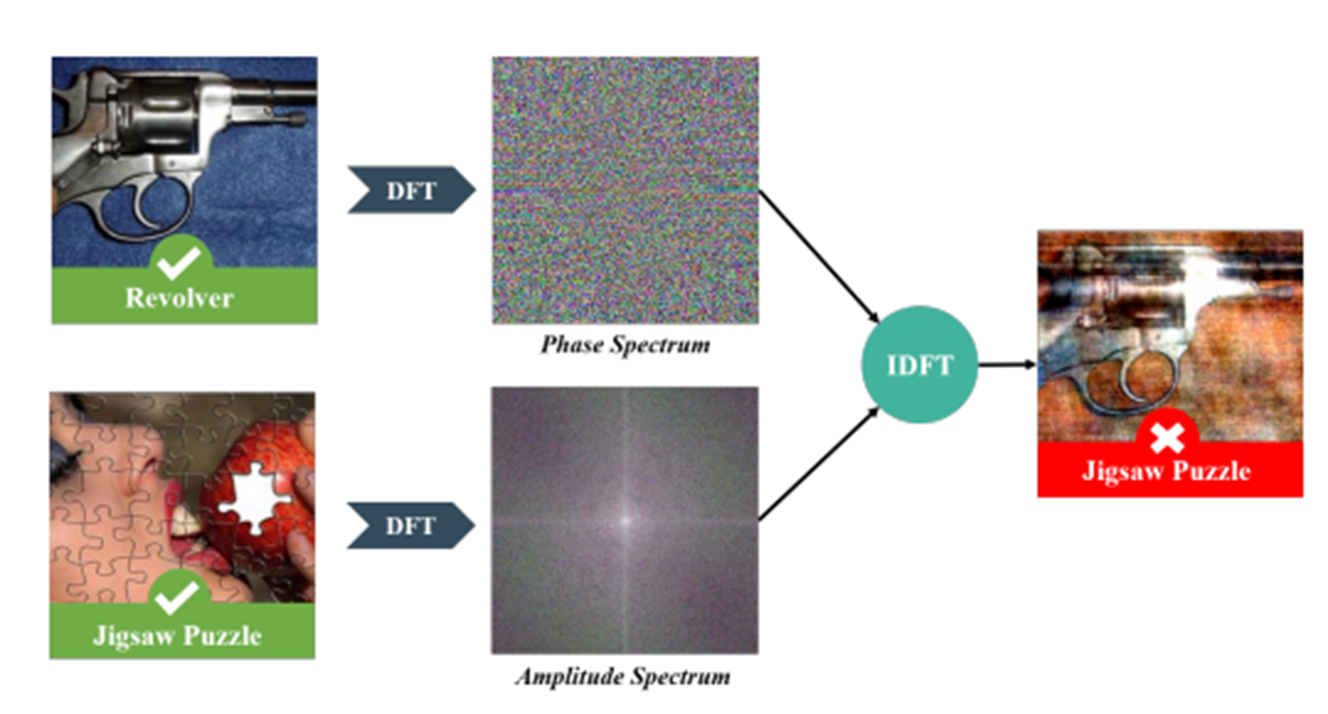
Amplitude-Phase Recombination paper
위 이미지는 CNN이 amplitude component에 얼마나 영향을 많이 받는지를 보여준다.
권총의 phase component와 직소 퍼즐의 amplitude component를 합쳐 새로운 이미지를 만들어냈을 때, 우리의 눈으로 보았을 때는 "저건 권총이네!"라고 인지하지만, 딥러닝은 직소 퍼즐로 예측하는 것을 알 수 있다.
3. The secret of CNN in the Frequency domain
CNN이 Frequency domain의 성분(phase, spectrum)와 어떠한 연관성이 있는지 좀 더 살펴보자.
Phase vs Amplitude in CNN

Amplitude-Phase Recombination paper
논문에서는 진행한 실험 중에 하나를 살펴보자.
위 이미지에서 $P$는 Phase, $A$는 Amplitude를 뜻하고 L, I, H는 각각 Low, intermediate, High frequency component를 뜻한다. 예를 들어, $\hat{P}^H_x$는 phase에서 high frequency 성분을 제외한 모든 영역을 제거한 것이라고 보면 도니다. 보통 이미지는 low > intermediate > high 순으로 포함되어있으니까 오른쪽으로 또는 아래쪽으로 갈수록 더 많은 정보를 잃은 것이라 보면 된다.
결국 이 이미지가 말하고 싶은 것은, CNN이 Phase와 Magnitude 성분 모두에게서 정보를 얻어내지만, phase보다는 amplitude에서 더 민감성을 보인다는 것이다. 즉, CNN은 Amplitude 정보에 더 치중되게 학습이 된다는 말이 된다.
Amplitude Property in common corruption and OODy

Amplitude-Phase Recombination paper
다음은 Common corruption과 out-of-distribution data의 high-frequency amplitude 성분에 대한 T-SNE 분포를 비교해본 것이다.
먼저 (a)는 원래 이미지(빨간색)와 그 이미지에 아주 작은 noise를 가한 이미지(회색)의 각각의 분포인데, 미세한 변화임에도 불구하고 분포가 많이 달라진 것을 알 수 있다. 즉, amplitude성분이 작은 corruption에도 민감하다는 것을 보여준다.
그 다음으로 (b)는 in-of-distribution(빨간색)과 out-of-distribution(회색)의 분포인데 각 데이터들을 구분하기가 거의 불가능한 것을 볼 수 있다. 이렇게 in-of-distribution과 out-of-distribution이 amplitude 성분에서 similarities를 갖기 때문에 딥러닝은 이들을 구분하는 것이 어려운 것이다.
Importance of Phase information
마지막으로 논문에서는 Phase 정보가 object를 인지하는데 얼마나 중요한 정보를 가지고 있는지를 보여준다.
이를 위해서 Discrete Fourier Transformation(DCT)을 살펴보자.
$$F_x(u,v) = \sum^N_{n=1} sum^N_{m=1} x(n, m) \cdot e^{i\theta}$$
$$= \sum^N_{n=1} sum^N_{m=1} x(n, m) \cdot (cos\theta + i \cdot sin\theta)$$
여기서 Real Part와 Imaginary Part로 나눠보면,
$$R_x(u,v) = \sum_{cos\theta \ge 0} cos\theta \cdot x(n, m) + \sum_{cos\theta \lt 0} cos\theta \cdot x(n, m)$$
$$I_x(u,v) = \sum_{sin\theta \ge 0} sin\theta \cdot x(n, m) + \sum_{sin\theta \lt 0} sin\theta \cdot x(n, m)$$
여기서 $cos\theta와 sin\theta$에 따라서 4가지의 template을 생각해볼 수 있는데, 이는
$$T^{R^+}_{u,v}(x) = max(cos\theta, 0), T^{R^-}_{u,v}(x) = max(-cos\theta, 0)$$
$$T^{I^+}_{u,v}(x) = max(sin\theta, 0), T^{I^-}_{u,v}(x) = max(-sin\theta, 0)$$
가 된다.
이 템플릿에 대해서 x와 multiplication을 하면 다음과 같은 examples가 나온다.
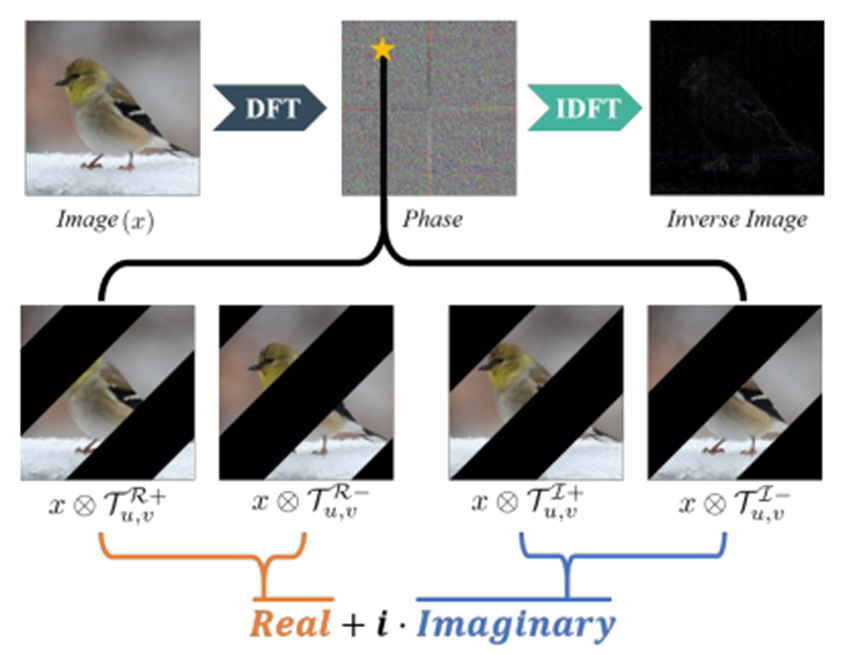
Amplitude-Phase Recombination paper
여기서 phase를 살펴보면,
$$ P_x(u,v) = arctan(\frac{\sum x \otimes T^{I^+}_{u,v} - \sum x \otimes T^{I^-}_{u,v}}{\sum x \otimes T^{R^+}_{u,v} - \sum x \otimes T^{R^-}_{u,v}})$$
즉, 위의 4가지 templates의 정보가 phase에 모두 포함되어있고, 이러한 정보를 사용해서, amplitude 정보가 없더라도, 이미지의 structured information을 복구해낼 수 있다. 이는 이미지의 spectrum을 변화시키더라도 이전 형태를 유지하는 현상에 대한 설명도 된다.
**리볼버 phase + 직소퍼즐 spectrum 이미지는 리볼버의 shape를 그대로 가지고 있다.
4. Amplitude-Phase Recombination(APR)
돌고 돌아서 드디어 본론이다...ㅎㅎ..결국 딥러닝 모델이 Amplitude 성분에서 많은 정보를 얻어내고, 이 amplitude는 corrouption에 sensitive하기 때문에 adversarial attack과 common corruption 등과 같은 현상이 일어난다.
그렇다면 직관적으로 생각했을 때, 이를 해결하는 방법은 무엇일까? 그렇다
CNN 모델이 amplitude 성분이 아닌 phase성분에 집중하여 학습되도록 유도하는 것이다.
그렇게 하기 위한 방법으로 Augmentation 기법을 제안하고 있고, 그 기법의 이름이 APR인 것이다.
간략하게 설명하자면, 이미지 $x_i$의 phase와 다른 이미지 $x_j$의 spectrum을 recombination하고, label을 $x_i$로 주는 것이다.
이전의 실험에서 보았듯이, 기존 모델은 spectrum의 label을 따라가는 경향이 있다. 따라서 위와 같은 데이터를 만들어 줌으로써 모델이 spectrum에 대한 정보를 최대한 무시하고 phase의 정보를 사용하여 label을 예측하도록 유도하는 것이다.
**phase의 정보를 사용하면 더 robustness한 모델을 얻을 수 있다고 생각하는 동기는 몇가지가 있다. 먼저, human visual system에서 robustness한 물체 인지를 위해서 phase정보를 사용한다. 그리고 위의 phase의 중요성에 대한 실험과 다크 프로그래머님이 phase와 spectrum 성분을 각 각 제거하여 보여주신 이미지를 보았을 때, phase는 object의 structured information을 포함하고 있고 spectrum은 보다 추상적인 feature를 가지고 있는 것을 알 수 있다.
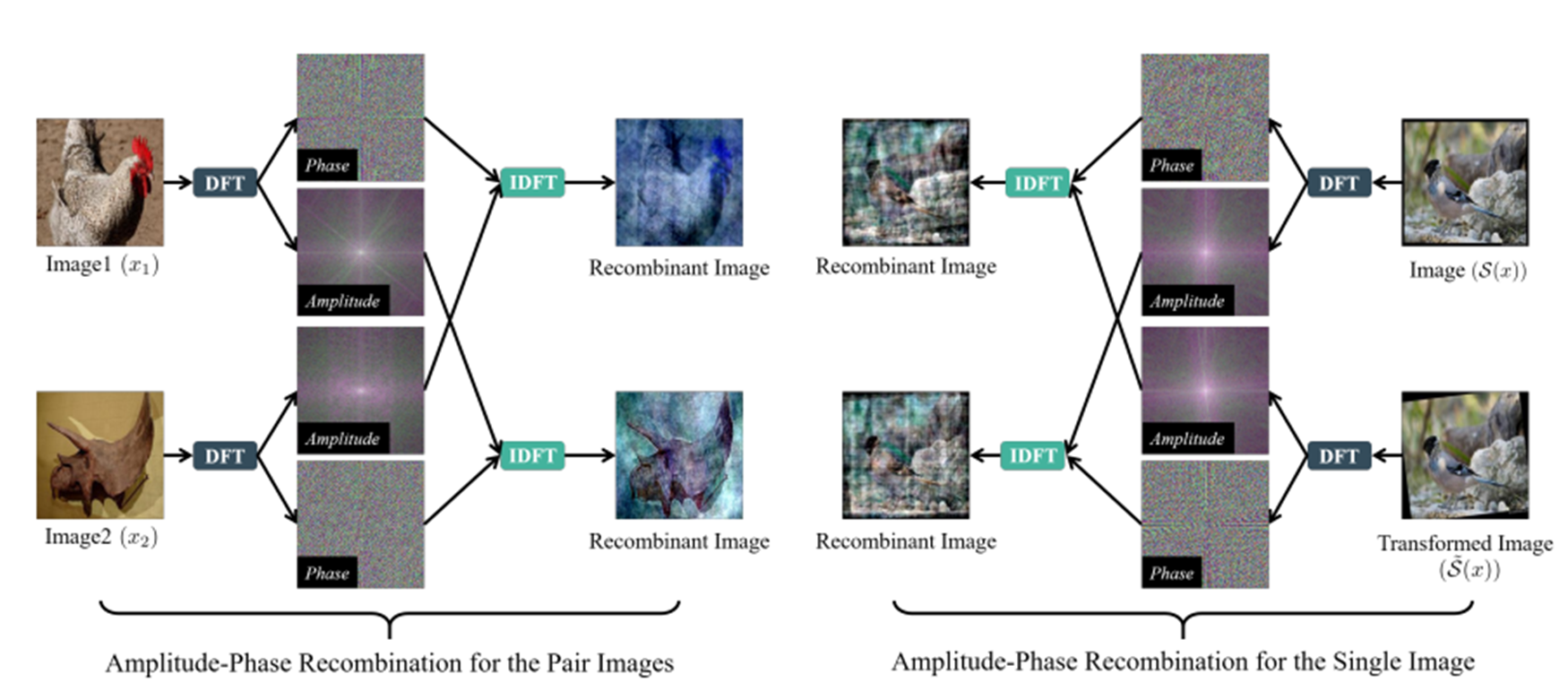
Amplitude-Phase Recombination paper
APR은 이미지가 pair인지 single인지에 따라서 APR-P와 APR-S로 나뉜다.
APR-P(왼쪽 이미지)는 서로 다른 클래스를 가지는 이미지 2개의 phase와 spectrum을 조합하는 것이고, APR-S(오른쪽 이미지)는 기존 이미지를 Transform시킨 이미지와 조합하는 방식을 말한다.
5. Experiments
실제로 성능은 어떠할까?
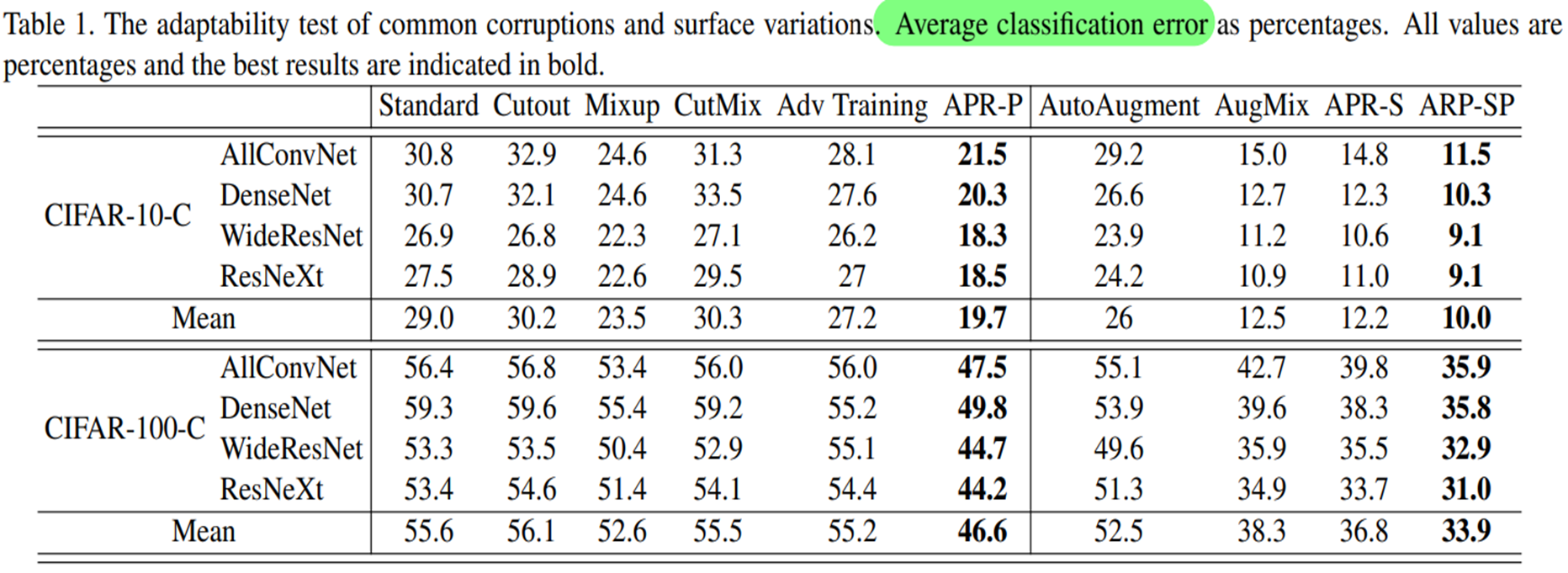
Amplitude-Phase Recombination paper
참고로 데이터셋에 붙은 C는 Corruption을 의미하고, 말그대로 corrupted(by noise, blur etc) 데이터셋을 의미한다.
위 표를 보았을 때, 다른 augmentation과 비교했을 때 더 roubst한 성능을 보여준다.
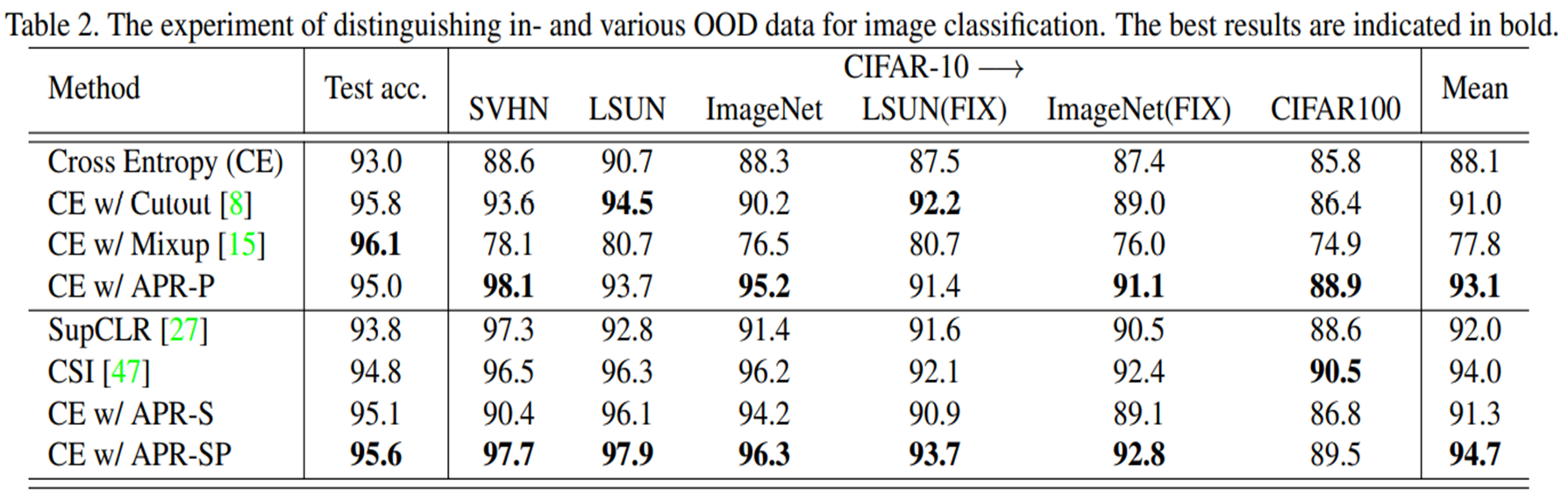
out-of-distribution data에 대한 성능도 좋은 것을 볼 수 있다. 참고로 여기서는 OOD detection에서 사용하는 AUROC라는 지표를 사용하였다.
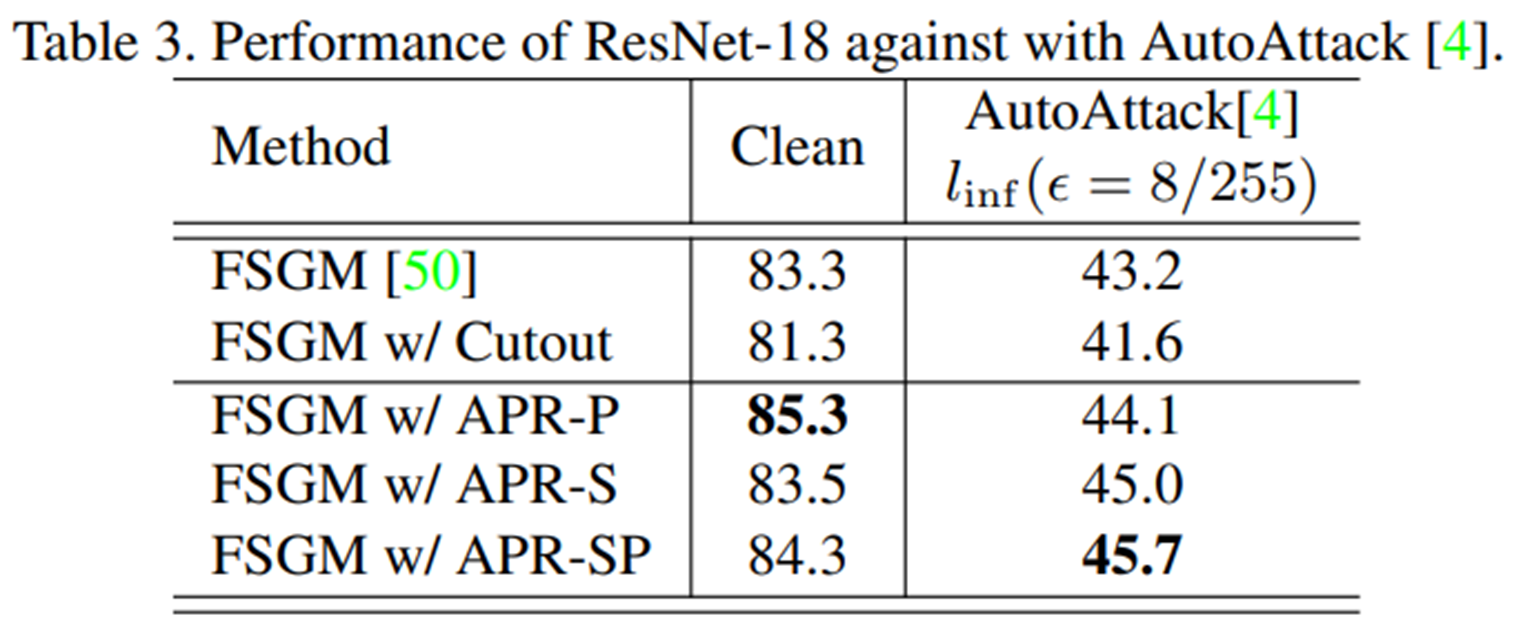
마지막으로 adversarial attack에 대한 성능인데, 주관적인 생각으로는 그렇게 큰 성능 향상은 없는 것으로 보인다. 그리고 method도 FGSM에 대한 adversarial training만 다루고 있으므로, 다른 method에 대해서도 동작할지는 미지수이다. attack에 대해서는 실험 내용이 빈약하지 않았나...라는 생각이 든다...왜일까...
이번 논문은 개인적으로 CNN이 adversarial attack이나 corruption에 민감한 현상을 frequency domain 관점에서 해석했다는 것이 흥미로웠다. 실제 성능이 어떻게 나올지는 미지수이지만, 배경이나 여러 가지 문제들을 직관적으로 와닿게 잘 설명했다고 생각한다. 기회가 되면 실제로 attack에 강한지 실험도 할 예정이다 ㅎㅎ