[인공지능 기초] 5. 퍼셉트론
인공지능이란 어디서부터 시작된 것일까? 한번 상상해보자!
사람같이 사고를 하는 기계를 만드려면 제일 먼저 떠오르는 부분은 무엇인가? 눈, 코, 입? 장기? 대부분의 사람들은 그것이 "뇌"라는 것을 바로 알아차릴 것이다.
이렇듯 초기 인공지능 붐을 불러왔던 학자들도 이 "뇌"와 "기계"를 연관지으려고 노력했고, 그 과정에서 최초의 인공지능 "퍼셉트론"이 등장하였다.

1. 퍼셉트론(Perceptron)

퍼셉트론이란, 인공 신경망의 초기 형태로 다수의 입력(X)으로부터 하나 또는 여러 신호(Y)를 출력하는 알고리즘이다. 이 개념은 인간의 뇌가 정보처리 하는 과정을 모방하여 만들어졌다.
퍼셉트론은 입력 노드(X)에서 출력 노드(Y)로 보내질 때, 각 입력도느 값들($x_1, x_2, \dots, x_n$ in X)에 고유한 가중치(Weight)가 곱해진다.
이 신호의 총합이 임계치를 넘으면 1, 아니면 0을 출력한다 => Activate Function
- $1 (w_1x_1 + w_2x_2 \gt theta(임계값))$
- $0 (w_1x_1 + w_2x_2 \le theta(임계값))$
여기서 가중치는 각 신호가 결과에 미치는 영향도를 조절하는 역할을 한다.
또한, 바이어스라는 개념도 사용하는데, 이 bias는 theta를 -b로 치환하여 넘긴 값이며, 뉴런의 활성화 임계치를 조절하는 역할을 한다.
2. 활성화 함수(Activate Function)
활성화 함수는 다양한 기능을 한다. 임계치에 따라 ON, OFF기능을 하거나 불필요한 값들을 필터링하기도 하고, 특정 목적으로 쓰이기도 한다. 여러 목적에 따라 사용하는 활성화 함수는 달라지며, 종류도 매우 다양하다.
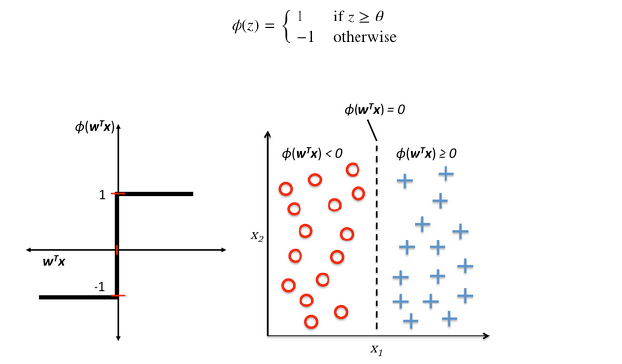
위와 같은 특정 목적 외에도 딥러닝에서 활성화 함수는 빠질 수 없는 존재이다. 그 이유는 선형 공간의 데이터를 비선형 공간으로 매핑 시켜주는 역할을 하기 때문이다. 만약 활성화 함수가 없다면 딥러닝을 아무리 깊게 만들더라도, 성능은 항상 제자리 걸음일 것이다.
**선형 함수를 계속해서 쌓더라도, 같은 선형함수로 표현이 가능하다.
**ex) $f(x) = ax+b, f(f(x)) = a(ax+b)+b = a^2x+ab+b, \ \ \ a^2=c, \ ab+b=d \ 라고 \ 치환하면 \ cx+d$
**그래서 보통 활성화 함수는 비선형 함수.
3. 계단함수와 논리회로
활성화 함수의 종류는 매우 많지만, 여기서는 퍼셉트론에서 사용한 간단한 계단 함수를 알아보겠다.
계단함수는 다음과 같이 구현할 수 있다.
import numpy as np
import matplotlib.pylab as plt
def step_function(x):
y = x >0 # x>0이면 true
return y.astype(np.int) # bool -> int
x= np.arange(-5.0,5.0,0.1) # -5.0~ 5.0 까지 0.1 단위로 배열 생성.
y = step_function(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1) # y축의 범위 지정
plt.show()
이제 위 계단 함수를 사용하여 AND, NAND, OR, XOR게이트를 만들어보고, 초기 인공지능이 어떠한 문제점을 가지고 있었는지 살펴보자.
3.1 AND 게이트
두 값이 모두 1일 때, 1을 출력, 그 외에는 0을 출력하는 게이트
def AND(x1, x2):
w1, w2, theta = 0.5, 0.5, 0.7 # give proper weight and threshold
tmp = x1*w1 + x2*w2
if tmp <= theta:
return 0
elif tmp > theta:
return 1
print(AND(0,0))
print(AND(0,1))
print(AND(1,0))
print(AND(1,1))
3.2 NAND 게이트
두 값이 모두 1일 때, 0을 출력, 그 외에는 1을 출력하는 게이트
import numpy as np
def NAND(x1, x2):
x = np.array([x1,x2])
w = np.array([-0.5, -0.5])
b = 0.7
tmp = np.sum(w*x)+b
if tmp <= 0:
return 0
elif tmp > 0:
return 1
print(NAND(0,0))
print(NAND(0,1))
print(NAND(1,0))
print(NAND(1,1))
3.3 OR 게이트
두 값이 모두 0일 때, 0을 출력, 그 외에는 1을 출력하는 게이트
import numpy as np
def OR(x1, x2):
x = np.array([x1,x2])
w = np.array([0.5,0.5])
b = -0.2
tmp = np.sum(x*w)+b
if tmp <= 0: return 0
elif tmp >0: return 1
print(OR(0,0))
print(OR(0,1))
print(OR(1,0))
print(OR(1,1))
3.4 XOR 게이트
위의 3개는 간단히 구현이 될 것이다. 하지만 XOR문제를 살펴보자.

출처 : https://trendy00develope.tistory.com/35
XOR 게이트는 두 값이 서로 다를 때, 1을 출력, 그 외에는 0을 출력한다. 다른 게이트와 같이 XW+B의 형태로 구현할 수 있는가? 불가능하다.
그 이유는 XOR 문제가 선형함수로 풀리지 않기 때문이다.
XOR문제를 풀기위해서는 다음과 같이 곡선을 사용하거나, 두 개의 직선을 사용해야 한다. 그래서 이러한 문제를 해결하기 위해 단층이 아닌 다층 퍼셉트론이 등장하였고, 문제를 고차원적으로 접근하는 방향으로 발전하였다. 이러한 방향으로 지금의 딥러닝이 탄생한 것이다(두둥).


출처(왼쪽) : https://poddeeplearning.readthedocs.io/ko/latest/%EB%B0%91%EB%B0%94%EB%8B%A5%EB%B6%80%ED%84%B0%20%EC%8B%9C%EC%9E%91%ED%95%98%EB%8A%94%20%EB%94%A5%EB%9F%AC%EB%8B%9D/2.Perceptron/
출처(오른쪽) : https://ehpub.co.kr/merchine-learning-perceptron-xor/